RESUMO
Redes Bayesianas é um método de modelagem e de decisão baseado em incerteza conhecida como redes de opinião, redes causais e gráficos de dependência probabilística, que combina probabilidade e conhecimento prévio do problema afim de determinar a probabilidade final de uma hipótese. Seus nós representam as variáveis (discretas ou contínuas), e os arcos representam conexões diretas entre eles.
Por pemitir uma abordagem interpretativa e analítica tem as Redes Bayesianas tem sido utilizada para:
- Estimação de risco operacional
- Diagnóstico médico,
- Credit scoring,
- Projeto de jogos computacionais,
- Imputação de dados, entre outras.
Desta forma, as Redes Bayesianas pode ser utilizada para fins de:
- Decisão
- Classificação
- Análise de dependência entre variáveis,
sendo uma alternativa às técnicas comumente utilizadas como, por exemplo, Regressão Logística e Análise Discriminante.
Uma Breve Revisão da Teoria de Probabilidades
Definição
A definição axiomática de probabilidade, dada por Komolgorov em 1933, é comumente adotada e considera que a probabilidade é uma função definida numa classe \(\tau\) de eventos de \(\Omega\) que satisfaz as seguintes condições:
\(P(A) \geq 0\)
Se \(\cap_{i=1}^{\infty} A\_i = \varnothing \Longrightarrow P( \cup_{i=1}^{\infty} A\_i) = \displaystyle \sum_{i=1}^{\infty} P(A\_i)\)
\(P(\Omega) = 1\).
Probabilidade condicional
A probabilidade condicional trata do fato de que muitas vezes temos conhecimento que um determinado evento já ocorreu, desta forma surge o interesse de calcular a probabilidade de outro evento de interesse e possivelmente relacionado ao evento anterior. Denotamos como P( E | F ) à probabilidade de ocorrência do evento E, sabendo que o evento F ocorreu, ou simplesmente, a probabilidade de E dado F. Desta forma, temos:
\(P(E|F) = \dfrac{P(E\cap F)}{P(F)}\)
Analogamente,
\(P(E\cap F) = P(E|F)P(F) ~~ \text{ou} ~~ P(E\cap F) = P(F|E)P(E)\)
generalizando, temos que:
\(\small P(E_1,E_2,\cdots,E_n) = P(E_1)P(E_2|E1)P(E_3|E_1,E_2) \cdots P(E_n|E_1, E_2, \cdots, E_{n-1})\)
então, podemos escrever que:
\(P(F) = \displaystyle \sum_{i=1}^{n} P(F|E_i)P(E_i)\)
Independência probabilística
Podemos considerar que os eventos E e F são independentes quando existe a relação.
\(P(E|F) = P(E) ~~ \text{ou} ~~ P(F|E) = P(F)\)
Teorema de Bayes
Como anteriormente, considere o evento \(F\) e \(E_i, \cdots , E_n\) eventos exclusivos e exaustivos, ou seja, que não possuem intersecção e que a união deles forma o espaço amostral. Assim, o Teorema de Bayes é definido por.
\(P(E_j | F) = \dfrac{P(E_j)P(F|E_j)}{\displaystyle \sum_{j = 1}^{n} P(E_j)P(F|E_j)}\)
O teorema de Bayes é uma junção do teorema de probabilidade condicional e da fórmula de probabilidades totais. Assim, \(P(E_j)\) pode ser denominada como probabilidade a priori, \(P( F ~ | ~ E_j )\) como verossimilhança e \(P(E_j ~|~ F)\) como probabilidade a posteriori, ou seja, a probabilidade posterior à observação do evento F. Além disso, o denominador é a decomposição de \(P(E)\) , ou seja, pode se considerado como constante normalizadora; desta forma, pode ser reescrito na forma.
\(P(E_j ~|~ F) ~ ~ \propto ~ ~ P (E_j) ~ P(F ~|~ E_j)\)
sendo \(~ \propto ~\) indicador de proporcionalidade. Em outros termos, podemos dizer que a probabilidade a posteriori é proporcional à probabilidade a priori multiplicada pela verossimilhança.
As distribuições Multinomial e Dirichlet
Estas duas distribuições, aqui introduzidas, são amplamente utilizadas no contexto de Redes Bayesianas quando métodos de estimação bayesiana são requeridos. Considere uma variável aleatória X discreta que represente um experimento com r possíveis resultados, sendo que cada tipo de resultado possui uma probabilidade específica \(P(X = x_i) = p_i ~ ~ \text{e} ~ ~ \displaystyle \sum_{i = 1}^{r} p_i = 1\). Além disso, o experimento é repetido de forma independente N vezes, de forma que a variável \(X_i\) seja o número de vezes que o resultado \(x_i\) está presente na amostra com \(i=1, \cdots,r\). Temos que a variável \(X\) segue distribuição Multinomial, sendo sua função densidade de probabilidade expressa pela fórmula.
\(P(X ~|~ N,~ p) ~ = ~ \dfrac{N!}{\displaystyle \prod_{i=1}^{r} x_i!} \displaystyle \prod_{i=1}^{r} p_i^{xi} ~ ~ ~ , ~ ~ ~ \text{em que} ~ ~ ~ \sum_{i=1}^{r} x_i = N\)
Considerando o termo \(\dfrac{N!}{\displaystyle \prod_{i=1}^{r} x_i!}\) como normalizador, temos
\(P(X ~|~ N,~ p) ~ \propto ~ \displaystyle \prod_{i=1}^{r} p_i^{xi}\)
Além disso, temos que para um vetor \(p=(p_1, p_2, ~\cdots ~,p_r)\) de valores desconhecidos com\(\displaystyle \sum_{i=1}^{r} p_i = 1\), podemos assumir que \(p\) segue distribuição Dirichlet com parâmetros \(\alpha = (\alpha_1, ~\cdots ~, \alpha_r)\) com \(\alpha_i > 1\), \(E(p_i) = \dfrac{\alpha_i}{\alpha_0}\) e função densidade de probabilidade expressa pela fórmula.
\(P(~ p ~|~ \alpha) = \dfrac{\Gamma(\alpha_0) }{\displaystyle \prod_{i=1}^{r} \Gamma(\alpha_i) } \displaystyle \prod_{i=1}^{r} p_i^{\alpha_i - 1}\)
em que podemos considerar o termo \(\dfrac{\Gamma(\alpha_0) }{\displaystyle \prod_{i=1}^{r} \Gamma(\alpha_i) }\) como normalizadorc, temos que:
\(P(~ p ~|~ \alpha) = \displaystyle \prod_{i=1}^{r} p_i^{\alpha_i - 1}\)
\(P(p ~|~ X) \propto \displaystyle \prod_{i}^{r} p_{i}^{\alpha_i + x_i - 1}\)
Notamos que neste caso a posteriori possui o mesmo tipo de distribuição que a priori, assim dizemos que a família Dirichlet é conjugada para amostras com distribuição Multinomial.
Redes Bayesianas
As Redes Bayesianas permite medir qual a influência probabilística não direta de uma variável para as demais, inclusive quando há um grande número de variáveis. Além disso, ela pode ser considerada como uma representação visual e informativa da tabela de probabilidade conjunta de todas as variáveis que envolvem o domínio do problema.
Elementos Básicos da Teoria de Grafos
A teoria de Redes Bayesianas é construída considerando grafos direcionados, conectados e acíclicos DAG (directed acyclic graph). O estudo dos grafos investiga as relações entre seus elementos, os nós e arcos. Os nós, círulos, representam as variáveis aleatórias do problema. Os arcos, setas, e representam a dependência probabilística direta entre duas variáveis.

Figure 1: Exemplo de Nó e Arco
Estruturas básicas existentes dentro da Teoria de grafos
O termo “direcionado” faz referência à presença de direção dos arcos, o termo “conectado” é utilizado para designar que todos os nós estão conectados na rede e, por fim, o termo “acíclico” se refere à propriedade de não retorno para um nó após seguida a direção dos arcos.

Figure 2: Estrutura básica
Da da figura acima, notamos que as Redes Bayesianas envolvem apenas alguns tipos de estruturas básicas:
- Estrutura de conexões simples: Existe apenas um caminho que liga uma variável a outra independente da direção dos arcos
- Estrutura de múltiplas conexões: Há mais de um possível caminho que liga uma variável a outra, independente da direção dos arcos.
A subdivisão das estruturas de conexão simples se dá pelo número de nós que originam a rede, ou seja, nós que não possuem nenhum arco chegando, apenas arcos partindo.
Hierarquia Entre Nós
A relação de dependência direta entre dois nós por meio do arco que os conecta é denominada por pai e filho, o nó de onde o arco parte é designado nó pai, o nó de onde o arco chega com sua ponta é designado nó filho. Além disso, um nó que não possui filhos é chamado de folha e um nó que origina a rede, ou seja, que não possui pais, é chamado de raiz.
Formalização Estatística da Estrutura
No contexto estatístico o termo nó A será substituído pelo termo variável A, a qual pode ser contínua ou discreta, apesar de alguns pesquisadores afirmarem que as Redes Bayesianas é primeiramente direcionada ao tratamento de variáveis discretas. Porém, as variáveis contínuas podem ser facilmente transformadas em variáveis discretas. Por exemplo, é condição básica a uma variável discreta não possuir variáveis pai contínuas. Neste contexto uma Rede Bayesiana é definida pelo trio \((\varepsilon, \theta, X )\), onde \(\varepsilon\) é uma estrutura DAG e \(\theta\) é um conjunto de parâmetros específicos de distribuições de probabilidades condicionais envolvendo um conjunto \(X\) de variáveis aleatórias discretas.
Tabela de probabilidade condicional
Outro elemento importante dentro da estrutura de Redes Bayesianas é a tabela de probabilidade condicional (CPT). Trata-se da exibição dos parâmetros de probabilidade condicional da variável sendo condicionada a seu(s) pai(s). Por exemplo, dado o conjunto de três variáveis A, B e C, todas dicotômicas assumindo valores binários, onde A e B são pais da variável C, temos a tabela abaixo.
| C | A | B | \(P(C \text{|} A,B)\) |
|---|---|---|---|
| 1 | 1 | 1 | \(\theta_1\) |
| 1 | 1 | 0 | \(\theta_2\) |
| 1 | 0 | 1 | \(\theta_3\) |
| 1 | 0 | 0 | \(\theta_4\) |
| 0 | 1 | 1 | \(\theta_5\) |
| 0 | 1 | 0 | \(\theta_6\) |
| 0 | 0 | 1 | \(\theta_7\) |
| 0 | 0 | 0 | \(\theta_8\) |
Exemplo Básico de uma Rede Bayesiana
Considere uma Rede Bayesiana dada sua estrutura já conhecida e relacionando seguintes variáveis binárias:
- Sexo { M, F };
- Idade { <20 anos, >= 20 anos };
- Créditos Anteriores { 1, >1 };
- Credit Rating { Bom , Ruim }
Assim, a rede é representada pela Figura abaixo:

Figure 3: Exemplo da Estrutura de Modelagem das Redes Bayesianas
Observando a figura acima que as variáveis
- Sexo,
- Idade,
- Créditos Anteriores,
- Credit Rating,
são representadas por seu respectivo nó na rede, sendo Sexo e Idade variáveis-pai da variável Crédtios Anteriores e Créditos Anteriores pai da variável Credit Rating. Ainda realizando uma análise hierárquica, as variáveis Sexo e Idade são classificadas na rede como variáveis-raiz e Credit Rating como folha.
Além disso, notamos que Sexo e Idade influenciam diretamente a variável Créditos Anteriores, que por sua vez influencia probabilisticamente de uma forma direta a variável Credit Rating. Interpretando os relacionamentos, se o cliente é do sexo masculino, ou não, isso influencia na probabilidade do cliente ter um, ou mais, créditos anteriores realizados na instituição. Se o cliente é menor de 20 anos, ou não, também influencia a probabilidade do cliente ter um ou mais créditos anteriores realizados na instituição. Assim, a probabilidade do cliente ter, ou não, realizado requisição de créditos anteriormente na instituição financeira influencia a probabilidade dele ser classificado como um bom pagador ou mau pagador. Para cada uma das variáveis e seus cruzamentos condicionais, temos uma tabela de probabilidade condicional (CPT) explicando numericamente a chance da cada categoria – evento – ocorrer dado premissas anteriores.

Figure 4: Rede Bayesiana tendo como evidencia a variável Idade (Idade <20)
Conceitos Importantes
Evidência
Dada a estrutura gráfica DAG, outra definição é importante para a teoria de Redes Bayesianas. Esta é denominada como evidência e refere-se ao fato de uma variável ser indicada pelo usuário da rede, ou seja, uma variável aleatória com valor conhecido e acoplado à Rede Bayesiana com estrutura já conhecida. Basicamente, podemos definir uma evidência com uma observação.
Considere o exemplo da Figura 2.3. Desta forma, observamos que um novo cliente possui a idade de 18 anos; assim, na rede, indicamos a variável Idade para a categoria respectiva, ou seja, definimos Idade <20 anos. A variável idade é classificada como uma evidência para a rede. A Figura 2.4 exibe uma demonstração visual para Idade <20 anos. As evidências são úteis quando existe o objetivo de realização de inferência probabilística para a rede em estudo. Este procedimento será visto com mais detalhes posteriormente.
As propriedades Markovianas
Assim como em alguns tipos de processos estocásticos, a dinâmica de uma Rede Bayesiana é controlada pela propriedade de Markov, a qual rege que não existem dependências diretas entre as variáveis de uma Rede Bayesiana que não estão explícitas através da apresentação orientada dos arcos, ou seja, cada variável possui dependência direta apenas de sua (s) variável (eis) pai.
A partir de todas as propriedades acima, temos que uma Rede Bayesiana é um par \((\varepsilon,\theta)\) definido sobre um conjunto de variáveis aleatórias \(X = \{ X_1, X_2, \cdots , X_k \}\), onde cada \(X_i\) corresponde a uma variável da rede, satisfazendo a propriedade de Markov:
\(P[X_i ~|~ X_j,~ pais(X_i)] = P[X_i ~|~ pais(X_i)]\)
Além disso, consideremos a distribuição de probabilidade conjunta de uma Rede Bayesiana com k variáveis e a propriedade (2.1), temos que em uma Rede Bayesiana \((\varepsilon,\theta )\) , definida sobre um conjunto de variáveis aleatórias \(X = \{ X_1, X_2, \cdots , X_k \}\), a probabilidade conjunta de toda a rede é dada através da expressão.
\(P(X_i = x_i, \cdots , X_k = x_k ) = \prod_{i = 1}^{k} P[X_i ~ | ~ pais(X_i) ]\)
Ou seja, as propriedades probabilísticas estão intimamente ligadas com o condicionamento da variável com seu (s) pai (s) respectivo (s). Note que (2.2) é resultado direto do desenvolvimento do Teorema de Bayes visto na seção 1.3.2.4., dada a propriedade (2.1).
Para o exemplo da Figura 2.3, a variável Sexo e Idade são independentes, pois não existe nenhum arco relacionando-as. Além disso, Credit Rating é diretamente independente de Sexo e Idade, a variável Credit Rating depende apenas diretamente da variável Créditos Anteriores, a qual é sua variável-pai.
Uma Rede Bayesiana na qual cada dependência probabilística entre as variáveis é dadapor um único arco é chamada de Rede perfeita (Korb e Nicholson, 2004).
Outro conceito muito utilizado na teoria de Redes Bayesianas é a cobertura de Markov, que consiste no conjunto formado pelas variáveis-pai, variáveis-filhos e pais dos filhos de uma determinada variável. Como exemplo, temos que a cobertura de Markov para a variável Idade da Figura 2.4 envolve a variável Créditos Anteriores (variável-filho da variávelIdade) e a variável Sexo (variável-pai de uma variável-filho da variável Idade), note que a variável Idade não possui variáveis-pai, se estas existissem seriam consideradas na cobertura de Markov. Outro exemplo de cobertura de Markov pode ser visualizado na Figura 2.5 que exibe a cobertura de Markov para a variável A.

Figure 5: Cobertura de Markov de A representada pelas variáveis-nó cinza
A propriedade de d-separação.
Através das propriedades markovianas, notamos que uma variável é independente de outra se não existe nenhum arco conectando-as. Porém, é possível definir independência quando existe entre as variáveis analisadas um grupo específico de variáveis, podendo ser um grupo de evidências, por exemplo. Neste caso, surge a conceito de d-separação. Para defini-la consideremos alguns tipos de conexões dadas em Neopolitan (2004). Seja X, Z e Y variáveis de uma Rede Bayesiana \((\varepsilon,V)\) , definimos alguns tipos de conexão:
- Se \(X ~ \rightarrow ~ Z ~ \rightarrow ~ Y\), temos um relacionamento head-to-tail;
- Se \(X ~ \leftarrow ~ Z ~ \rightarrow ~ Y\), temos um relacionamento tail-to-tail;
- Se \(X ~ \rightarrow ~ Z ~ \leftarrow ~ Y\), temos um relacionamento head-to-head
Além disso, podemos definir \(A \subset \vee\), sendo \(X e Y \in \vee - A\). Desta forma, para os casos 1 e 2, se consideramos que \(Z \in A\) , a variável \(Z\) bloqueará o caminho entre \(X ~\text{e}~ Y\). Para o caso 3, se consideramos que Z e seus descendentes A, a variável Z bloqueará o caminh entre X e Y. Se o caminho entre duas variáveis, ou conjunto de variáveis, é bloqueado, dizemos que essas variáveis, ou conjuntos, são d-separados. A Figura 2.6, retirada de Marques e Dutra (1999), ilustra os três casos de d-separação, onde os conjuntos U e W são d-separados.

Figure 6: Tipos de d-separação, U e W d-separados
Equivalência de Markov
Existem inúmeras estruturas possíveis no enredo de Redes Bayesianas. Porém, podemos construir para cada conjunto de variáveis um grupo de estruturas extremamente semelhantes, chamadas de equivalentes de Markov. Segundo Neapolitan (2004), dois grafos são equivalentes quando mantêm as mesmas independências condicionais. Ou seja, dois grafos são considerados equivalentes quando conservam as mesmas ligações de arcos entre as variáveis independente da direção, com exceção às ligações head-to-head, ou seja, quando uma variável-filho possui mais que uma variável-pai. Assim, considere o exemplo da Figura 2.7.

Figure 7: Exemplo de identificação de redes Bayesianas Markov equivalentes
Analisando a Figura 2.7, notamos que a estrutura (a) não é equivalente a (b), pois além de não preservar a conexão head-to-head \(C ~ \rightarrow ~ E ~ \leftarrow ~ D\) , a estrutura (b) não mantém a conexão entre as variáveis A e B. Esses mesmos motivos fazem (b) não equivalente à estrutura (c). Comparando a estrutura (a) com (c), notamos que existe apenas diferença entre a direção de ligação entre as variáveis A e B, ou seja, (a) e (c) são equivalentes. Dizemos que (a) e (c) pertencem à mesma classe de equivalência markoviana.
Método Geral para a Construção de uma Rede Bayesiana.
A construção de uma Rede Bayesiana não é trivial, além de existir vários métodos para a estimação de estruturas de rede através do conjunto de dados, os métodos podem ser influenciados por fatores como a ordem e escolha das variáveis que compõem o problema. Esse problema proporciona atualmente intensas pesquisas buscando um método ótimo para estimação de estruturas DAG para domínios de problemas práticos. Porém, de uma forma geral, Pearl (1988) criou um algoritmo baseando-se nas propriedades 2.1 e 2.2, no qual, dado um conjunto de variáveis discretas ordenadas, constrói uma Rede Bayesiana única, adicionando às variáveis a rede em sua ordem e acrescentando arcos para a formação da estrutura. Assim, cada variável é conectada às variáveis antigas da rede, o que garante que a estrutura seja sempre acíclica.
O algoritmo de Pearl é dado abaixo.
- Escolha um conjunto de variáveis \(X_i\) que em suposição descreva o problema;
- Escolha uma ordem para as variáveis;
- Para todas as variáveis em ordem, faça:
- Escolha a variável \(X\) e adicione-a na rede;
- Determine os pais da variável \(X\) dentre os nós que já estão na rede, que satisfaça \(P[X_i~|~ X_j,~ pais(X_i)] = P[X_i| pais(X_i)]\)
- Construa a tabela de probabilidade condicional (CPT) para X.
Para uma Rede Bayesiana ser adequada, ela deve ser perfeita, ou seja, todos arcos devem expressar corretamente as dependências entre as variáveis. Desta forma, é fácil notar que para a construção de uma Rede Bayesiana devemos escolher uma ordem correta para as variáveis, pois diferentes ordens podem gerar Redes Bayesianas diferentes. Desta forma, Korb e Nicholson (2004) sugerem que primeiramente consideremos as variáveis possíveis a serem raízes e suas variáveis independentes, a seguir as demais variáveis. Outros métodos de construção de Redes Bayesianas serão apresentados no decorrer do trabalho.
Resumo
Inferência em Redes Bayesinas
No contexto de Redes Bayesianas, o termo “inferência”, também conhecido como atualização de crença (belief updating), é comumente utilizado para referenciar a atualização de probabilidades por toda a estrutura da rede dada um conjunto de evidências. Ou seja, segundo Korb e Nicholson (2004), trata-se de um mecanismo para cálculo da distribuição posteriori de probabilidade para um conjunto de variáveis, dado um conjunto de evidências, ou seja, variáveis aleatórias com valores instanciados.
Porém, como visto anteriormente, existem diversos tipos de estruturas de Redes Bayesianas, assim as inferências probabilistas podem ser realizadas de diferentes formas assumindo tipos de estruturas específicas e com diferentes quantidades de variáveis.
Entretanto, existem fatores que dificultam o processo de inferência, como a complexidade da estrutura em análise e o número de variáveis. Ou seja, para poucas variáveis e uma estrutura gráfica dirigida acíclica (DAG) não complexa, a propagação das probabilidades pode ser facilmente calculada. À medida que existe um grande número de variáveis e estruturas mais complexas, existe grande dificuldade no cálculo das probabilidades da rede.
Marques e Dutra (1999) consideram que existe maior dificuldade quando o problema é modelado de uma forma complexa, ou seja, quando a estrutura considerada para a inferência possui relações complexas entre as variáveis. Assim, em algumas situações, uma rede com apenas uma dezena de variáveis pode necessitar de um tempo computacional muito grande para término da inferência (às vezes inviável), enquanto uma rede contendo milhares de variáveis e uma estrutura simplista pode levar apenas alguns instantes de processamento.
Buscando contornar tal problema, utilizamos algoritmos de inferência probabilística que facilitem os cálculos, sendo essa uma área de pesquisa em Redes Bayesianas.
Deste modo, alguns algoritmos são utilizados de forma particular para tipos gerais de estruturas, basicamente as estruturas citadas na seção 2.1.2. Considerando as estruturas mais comuns, existem dois tipos de algoritmos para realizar inferência probabilista, estes são chamados de algoritmos exatos e algoritmos aproximados. Os algoritmos exatos produzem resultados mais satisfatórios, porém exigem um grande esforço computacional na presença de um alto número de variáveis na rede. Os algoritmos aproximados são construídos através de métodos de simulação, tendo uma precisão inferior, porém maior velocidade de processamento que os algoritmos exatos.
Neste capítulo, serão expostos os mais comuns tipos de algoritmos exatos e aproximados, bem como suas utilizações em diferentes tipos de estruturas de Redes Bayesianas.
Algoritmo de Inferência Exata
Aplicação: Fatores de Risco em Trombose Coronária
Conjunto de Dados
O conjunto de dados contém 6 variáveis com prováveis fatores de risco para trombose coronária, compreendendo dados de 1841 homens.
#Coleta da Base de Dados Coronary
coronary <- bnlearn::coronary %>% data.frame()
str(coronary)## 'data.frame': 1841 obs. of 6 variables:
## $ Smoking : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ M..Work : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ P..Work : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ Pressure: Factor w/ 2 levels "<140",">140": 1 1 1 1 1 1 1 1 1 1 ...
## $ Proteins: Factor w/ 2 levels "<3",">3": 1 1 1 1 1 1 1 1 1 1 ...
## $ Family : Factor w/ 2 levels "neg","pos": 1 1 1 1 1 1 1 1 1 1 ...
- Smoking ( Tabagismo ).
- M. Work ( Trabalho mental extenuante ).
- P. Work ( Trabalho físico extenuante ).
- Pressure ( Pressão arterial sistólica ).
- Proteins ( Proporção de beta e alfa lipoproteínas ).
- Family ( Anamnese familiar de doença coronária ).
Estrutura de Aprendizagem
Existem vários algoritmos de aprendizagem de estruturas em Redes Bayesianas e alguns estão disponíveis no pacote bnlearn, vamos utilizar o algoritmo Hill Climbing.
# Aprendizagem da rede bayesiana usando algoritmo Hill-Climbing (HC)
res <- hc(coronary)A representação gráfica abaixo mostra a relação de dependência condicional entre as variáveis.
#Plot da Rede
plot(res)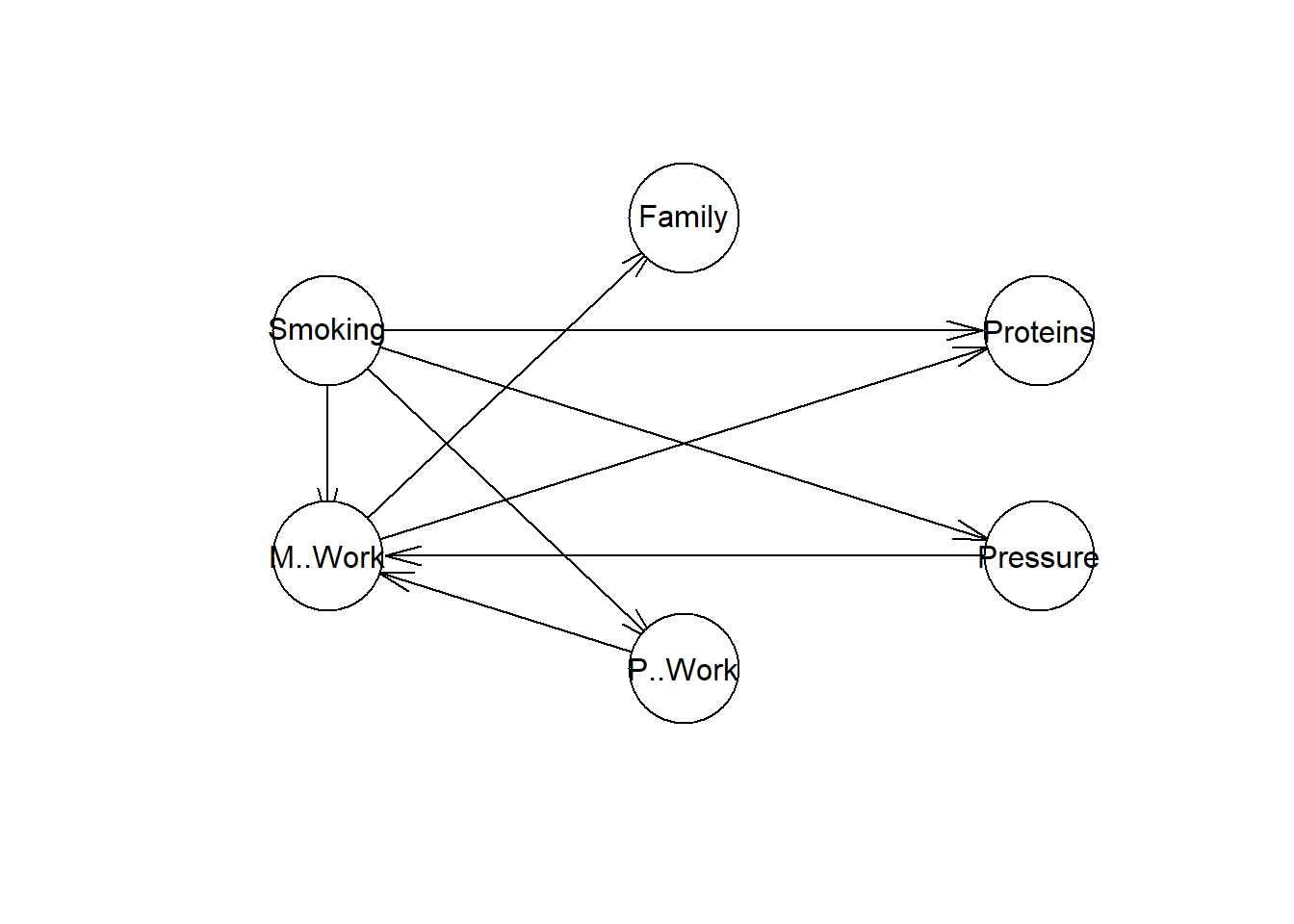
Observe como o nó Pressure é influenciado pelo nó Smoking. No entanto, não faz muito sentido o nó Family, ser influenciado pelo nó M. Work, e neste caso, vamos modificar a estrutura gerada removendo o link entre os nós M. Work e Family.
#Remover o Link entre nós "M..Work", "Family"
res <- drop.arc(res,"M..Work","Family")
#Plot da Rede
plot(res)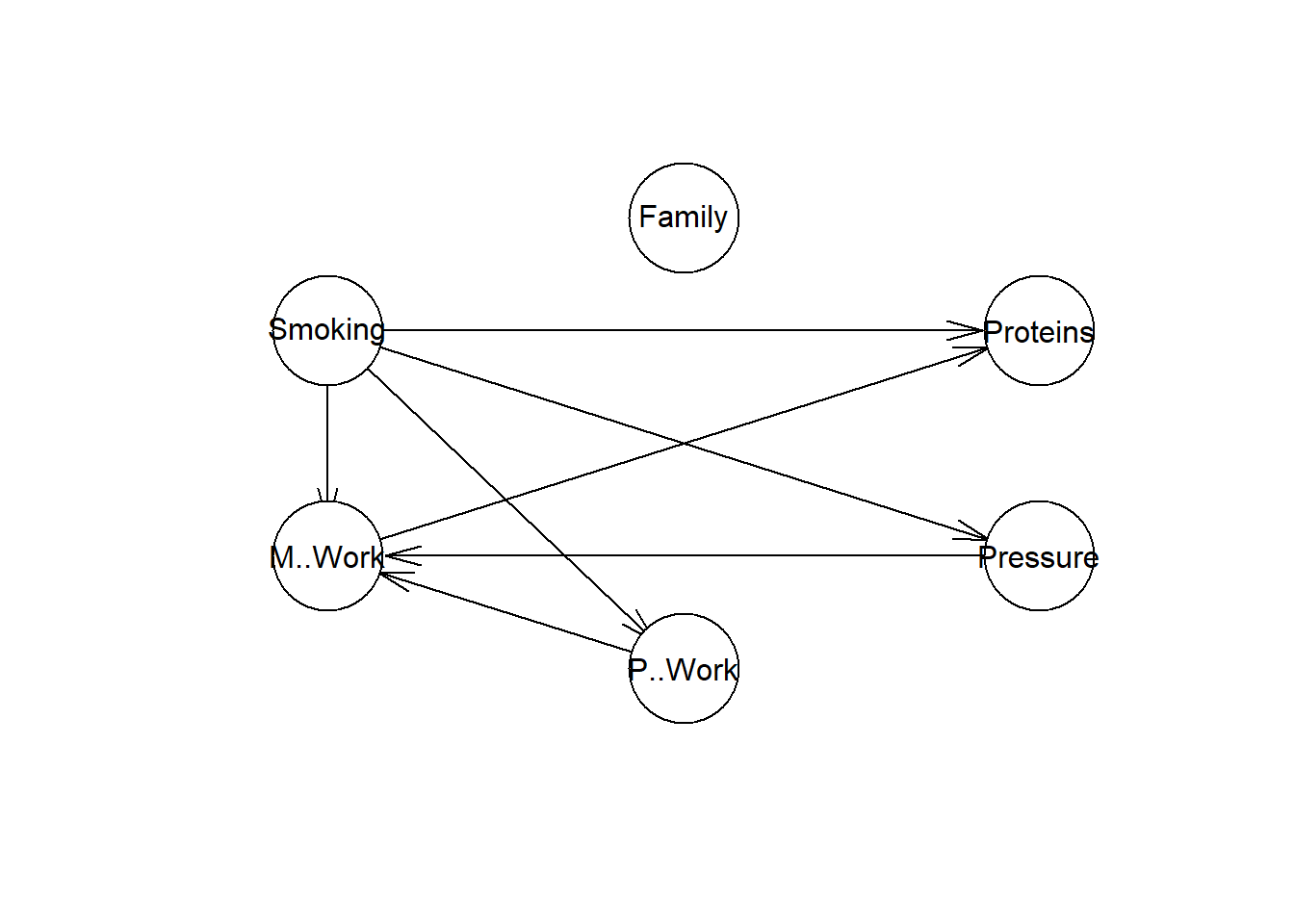
Tabelas de Probabilidade Condicional.
A função bn.fit nos retorna as tabelas de probabilidade condicional ( CPTs ) em cada nó, calculado pelo algoritmo EM (Expectation–Maximization).
#Rede Bayesiana Ajustada
bnfit <- bn.fit(res, data = coronary)Analisando as probabilidades condicionais geradas para o nó Pressure (Pressão).
#Tabela de Probabilidade Condicional - Pressure
bnfit$Pressure##
## Parameters of node Pressure (multinomial distribution)
##
## Conditional probability table:
##
## Smoking
## Pressure no yes
## <140 0.5359001 0.6125000
## >140 0.4640999 0.3875000Observe que o nó Pressure é condicionado a variável Smoking, conforme a representação gráfica da Rede Bayesiana.
Extraindo valor da Análise.
As Redes Bayesianas nos permite a atualização das probabilidades de toda a estrutura da rede dada um conjunto de evidências através da distribuição de probabilidade a posteriori dado um conjunto de variáveis.
O processo de inferência podem ser realizado sobre as Redes Bayesianas, em quatro maneiras distintas:
- Diagnósticos: partindo dos efeitos para as causas;
- Causa: partindo das causas para os efeitos;
- Intercausal: entre causas de um efeito comum;
- Mistas: combinação de dois ou mais tipos descritos acima.
Probabilidades de um evento.
Comparar as probabilidades de um indivíduo ter Pressure > 140 para cada nível da variável Smoking dado que Proteins é ‘>3’.
#Inferência em Redes Bayesianas
100 * cpquery(bnfit,
event = (Pressure==">140"),
evidence = (Smoking=="yes" & Proteins=='>3')) %>% round(2)## [1] 40100 * cpquery(bnfit,
event = (Pressure==">140"),
evidence = (Smoking=="no" & Proteins=='<3')) %>% round(2)## [1] 48$ P(Pressure > 140 ~ | ~ Smoking = yes, ~ Proteins > 3) = 41 % $ $ P(Pressure > 140 ~ | ~ Smoking = no , ~ Proteins > 3) = 47 % $
